최근 필자가 정렬과 관련된 알고리즘을 개요정도만 익히고 Python으로 직접 코드를 구현해보는 일이 몰두하고 있다. IT 기술 분야는 백 번 듣는 것 보다는 한 번 보는게 낫고, 백 번 보는 것보다는 한 번 해 보는것이 낫다는 것을 이미 일을 해 오면서 느껴왔었기 때문이다. 물론, 고생은 조금 많이 하고 있다. 아무래도 컴퓨터를 전공한 사람이 아니라 야매(?)로 개발을 시작했다보니, 컴퓨터처럼 논리를 만드는 일에 있에서는 확실히 버벅일 수 밖에 없다.
이번 포스팅에서는 자료를 정렬하는 알고리즘 중 하나인 삽입 정렬(Insertion Sorting)에 대해 알아보려한다. 다른 기본 알고리즘은 몇몇 빼고 구현이 크게 어렵지 않았는데, 삽입 정렬은 필자가 논리를 영 이상하게 세워버리는 바람이 그 논리 회로 뜯어고친다고 상당히 고생을 많이 했기 때문에 먼저 다루어보려한다.
1. 삽입 정렬 (Insertion Sorting) 개요
삽입 정렬은 버블 정렬과 유사하게, 비교를 진행할 원소를 배열 내에서 순차적으로 단방향 스캔하여 선택한다. 단, 배열의 양 끝단은 선택에서 제외한다.
7, 3, 5, 8, 4 라는 배열이 있고 오른쪽으로 단방향 스캔을 진행하는 경우,
-> 3 선택 및 원소 비교
-> 5 선택 및 원소 비교
-> 8 선택 및 원소 비교
-> 4 선택 및 원소 비교
순으로 진행한다. 뭔가 이상한 점이 하나 느껴질텐데, 가장 좌측의 7은 선택 대상에서 제외된다는 것이다.
눈치채신 분들도 있겠지만, 삽입 정렬에서 선택된 값과 비교되는 대상은 선택된 원소의 좌측에 위치한 원소들이다 (물론, 좌측 스캔을 진행한다면 선택된 원소의 오른쪽이 비교 대상 원소가 된다).
선택한 원소의 비교는 아래와 같이 진행된다.
[ 3 선택 시 ]
7, 3, 5, 8, 4
-> 좌측에 위치한 원소의 첫 번째 값인 7과 대소 비교
-> 3이 7보다 작으므로 두 원소의 자리 교체.
3, 7, 5, 8, 4
-> 비교 종료
[ 5 선택 시 ]
3, 7, 5, 8, 4
-> 좌측에 위치한 원소의 첫 번째 값인 7과 대소 비교
-> 5가 7보다 작으므로 두 원소의 자리 교체
3, 5, 7, 8, 4
-> 좌측에 위치한 원소의 두 번째 값인 3과 대소 비교.
-> 3보다 5가 크므로 두 원소의 자리 교체 없음.
3, 5, 7, 8, 4
-> 비교 종료
...
이러한 비교가 배열의 크기인 N보다 1번 적게 수행되면 배열 내 모든 원소는 오름차순으로 배열이 완료된다. 비교 과정을 세세하게 살펴보면 바로 옆에 위치한 원소와 버블 정렬(Bubble Sorting)을 통해 대소 비교 및 자리 교체를 진행하는 것을 확인할 수 있다.
가끔 일부 삽입 정렬을 소개하는 책이나 글을 보면 아래의 그림처럼 선택 대상 원소를 추출한 뒤, 원소가 추출된 Index와 추출된 원소가 삽입될 Index 사이의 원소를 오른쪽으로 옮기는 형태로 설명하는 경우가 있다.

뭐... 버블 정렬이 완료된 상태에서 결과를 보면 전혀 틀린 설명은 아니다만, 저 이동 과정이 버블 정렬의 결과라는 설명이 없다면 오해하기가 딱 좋은 그림이다. 버블 정렬을 쓰지 않고 위의 그림대로 코드를 작성하면 정렬이 안 되는 것은 아닌데, 선택을 위한 Loop 1개, 대소 비교를 위한 Loop 1개, 이동을 위한 Loop 1개, 즉 3개의 Loop를 중첩해서 사용해야 한다. 이 말은 코드를 수행하는데 있어 시간복잡도가 O(N^3)으로 '매우' 증가한다는 것이다.
필자는 위의 잘못 이해한 논리로 코드를 구현하면서 "개요에서 삽입 정렬이 O(N^2)의 시간복잡도를 가지는데 왜 내 코드는 O(N^3)가?" 라는 물음에 빠져버려 계속 허우적댔었다.
2. 삽입 정렬 코드 구현
그럼, 삽입 정렬도 개요에서 설명한대로 구현을 해보자. 늘 그래왔듯이 뼈대부터 작성할 것인데, 단순한 정렬이므로 함수 하나만으로도 충분하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def insertion_sort(arr: list):
len_arr = len(arr)
# 원소 선택을 위한 Loop문
for idx in range(1, len_arr):
pass
"""
큰 수부터 오른쪽에 배치하려면
for idx in range(len_arr - 1, -1, -1):
pass
"""
|
cs |
배열에서 선택할 원소를 스캔하는 방향을 어떻게 지정하느냐에 따라 for 문의 범위와 내부 비교문이 달라지게 된다. 만약 개요와 달리 오른쪽부터 선택 값을 스캔한다면 아래의 for문을 사용해야 한다. 우선 필자는 우측으로 스캔하는 Loop로 코드를 작성하려 한다.
for 문에서 선택된 배열 Index의 원소와 좌측 원소를 비교하는 코드를 작성해보자. 먼저 선택된 Index의 좌측에 있는 원소 모두와 비교를 거쳐야하기 때문에 내부에 for 문이 하나 더 추가된다.
|
1
2
3
4
5
6
7
8
9
10
11
|
def insertion_sort(arr: list):
# 전체 배열 길이 저장
len_arr = len(arr)
# 원소 선택을 위한 Loop문
for idx in range(1, len_arr):
# 좌측 원소와의 대소 비교를 위한 Loop 문
for cpm_idx in range(idx, 0, -1):
pass
|
cs |
안쪽의 for 문에 print()로 idx와 cpm_idx 값을 출력해보자.

외부 Loop에서 선택된 Index와 내부 비교 대상 Index가 위의 개요에서 설명한 삽입 정렬 논리대로 잘 출력됨을 알 수 있다. 이제 여기에 값을 비교하는 코드를 작성해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
def insertion_sort(arr: list):
# 전체 배열 길이 저장
len_arr = len(arr)
# 원소 선택을 위한 Loop문
for idx in range(1, len_arr):
# 좌측 원소와의 대소 비교를 위한 Loop 문
for cpm_idx in range(idx, 0, -1):
if arr[cpm_idx] < arr[cpm_idx - 1]:
arr[cpm_idx], arr[cpm_idx - 1] = arr[cpm_idx - 1], arr[cpm_idx]
|
cs |
이 코드에도 진행 상황을 출력하는 코드를 추가한 뒤 실행하면 아래와 같은 결과가 나온다.

스크린 샷이 길어져서 최종 결과까지 출력하지 않았지만, Loop가 실행됨에 따라 배열 내부가 오름차순으로 정렬되고 있음을 알 수 있다.
만약 스캔의 방향을 반대로 진행하고 싶다면 아래와 같이 코드를 수정하면 된다.
|
1
2
3
4
5
6
7
8
9
10
|
def insertion_sort(arr: list):
# 전체 배열 길이 저장
len_arr = len(arr) - 1
for idx in range(len_arr - 1, -1, -1):
for cpm_idx in range(idx, len_arr):
if arr[cpm_idx] > arr[cpm_idx + 1]:
arr[cpm_idx], arr[cpm_idx + 1] = arr[cpm_idx + 1], arr[cpm_idx]
|
cs |
전체 배열 길이인 len_arr 값이 하나 줄어든 것이 보이는데, 원소를 선택할 때, 최우측의 원소는 제외를 해야 하기 때문이다. 그리고 내부 Range 문도 비교 범위를 지정함에 있어서 1씩 감소된 값이 추가된 것도 주의하자. 결과는 우측 스캔으로 작성한 첫 번 째 코드와 동일하게 나타난다.
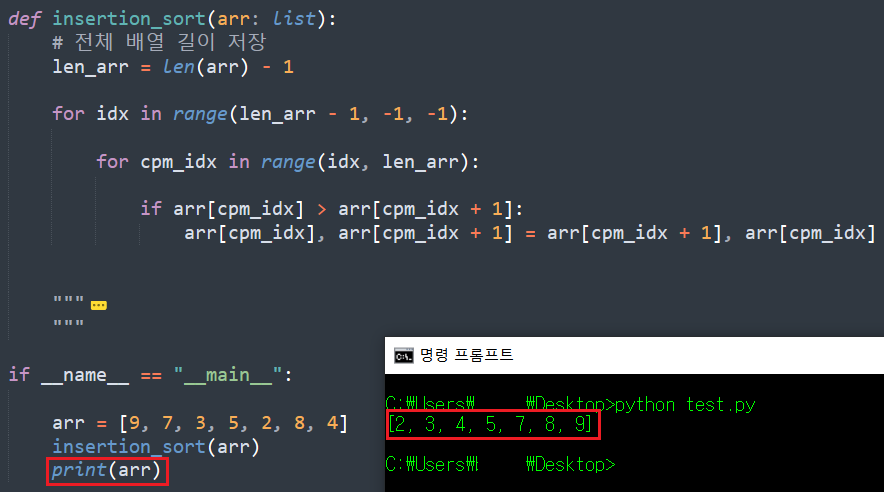
3. 잘못된 논리로 작성한 삽입 정렬의 수행 시간 확인
원래 포스팅 끝내려했는데, 심심해서 테스트를 더 해보려한다. 필자가 처음에 잘못 이해한 삽입 정렬 방식을 코드로 작성하면 어떻게 될까? 이건 중간 과정 생략하고 바로 코드를 작성해보려한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
def wrong_insertion_sort(arr: list) -> None:
len_arr: int = len(arr)
# 배열 내 원소 선택을 위한 스캐닝 Loop
for idx in range(1, len_arr):
moving_range_left = idx
tmp_value = arr[idx]
# 배열 내 마지막 변경 위치 파악을 위한 Loop
for cmp_idx in range(idx, 0, -1):
if arr[idx] < arr[cmp_idx - 1]:
moving_range_left = cmp_idx - 1
if moving_range_left != idx:
# 배열 내 이동이 필요한 원소의 우측 이동 Loop
for move_idx in range(idx - 1, moving_range_left - 1, -1):
arr[move_idx + 1] = arr[move_idx]
# moving_range_left Index에 선택값 추가
arr[moving_range_left] = tmp_value
|
cs |
코드의 결과는 제대로 된 논리로 구현된 코드와 마찬가지로 문제없이 잘 나타나는 것이 확인된다.

그렇지만 위의 코드는 필자가 서두에 언급한대로 for 문을 최대 3번을 돌아야하는 구조이다 보니, 시간 복잡도 측면에서는 좋은 코드가 아니다. 지금이야 필자가 많지 않은 데이터를 정렬하는 예시만 보여서 간간히 잘못 구현된 코드가 더 빠른 연산을 수행하는 경우가 종종 있긴 한데, 데이터의 양이 많아지거나 반복 횟수가 증가하면 당연히 잘못된 논리로 작성된 코드는 수행 시간이 길어질 수 밖에 없다.
그럼, 제대로 된 논리로 구현된 코드와 잘못된 논리로 작성한 코드는 수행 시간에 있어서 큰 차이를 보이는 지 확인해보자. 필자는 timeit 모듈을 사용해서 각 함수를 100만 번 수행한 시간을 측정해보려한다.
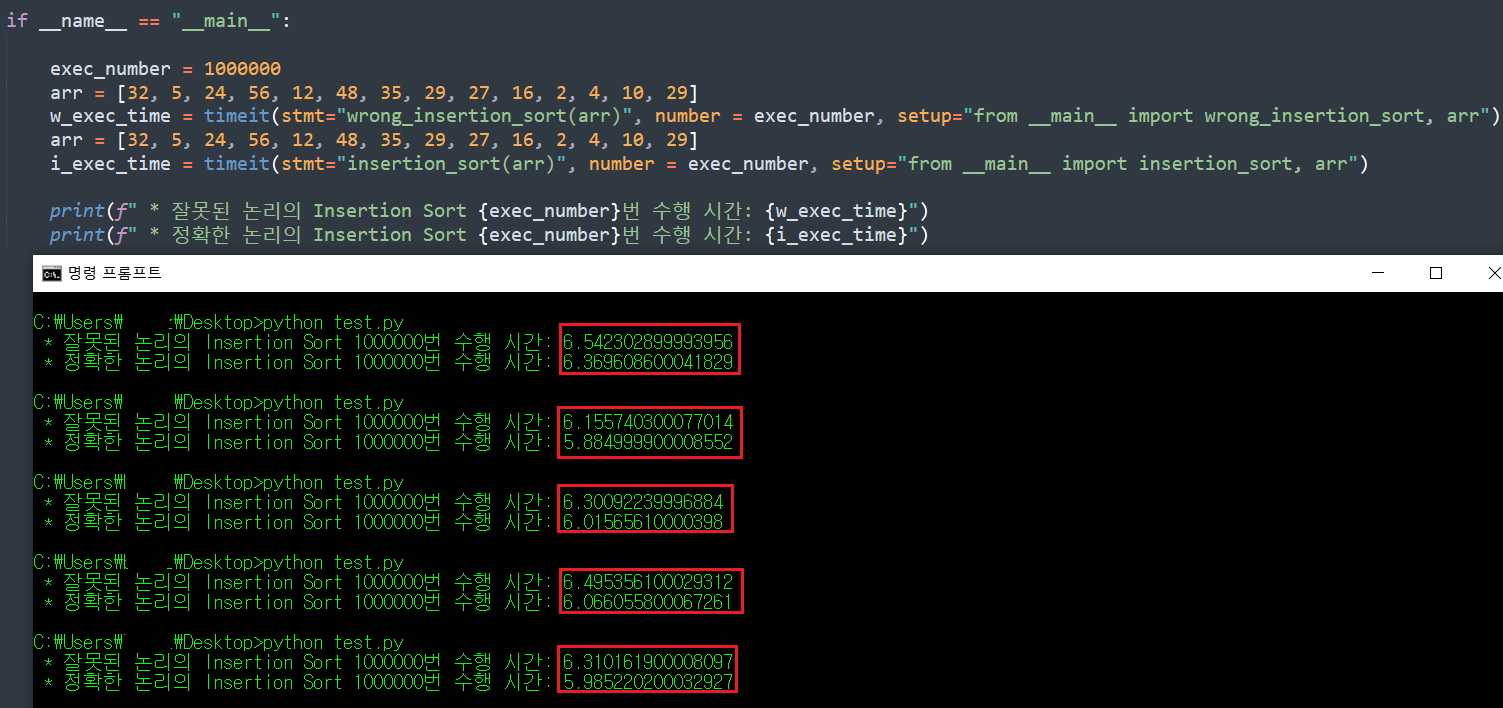
함수 반복 수행이 백만번 가까이 되니, N^2의 삽입 정렬 코드가 잘못된 논리로 작성된 코드보다 항상 빨리 종료됨을 확인할 수 있다.
다음 포스팅은, 필자가 삽입 정렬을 조금 더 개선할 수 있는 방법을 찾으면 그와 관련된 포스팅을 진행할 것이고, 아니면 선택 정렬에 대해 글을 작성해보려한다.
End.
'Python > Python Data Structure and Algorithm' 카테고리의 다른 글
| [자료구조 with Python] 12 - 정렬 알고리즘(5), 병합 정렬(Merge Sort) (0) | 2024.03.13 |
|---|---|
| [자료구조 with Python] 11 - 정렬 알고리즘(4), 선택 정렬(Selection Sort) (0) | 2024.03.12 |
| [자료구조 with Python] 9. 정렬 알고리즘(2) - 버블 정렬과 Shaker 정렬 (0) | 2024.03.08 |
| [자료구조 with Python] 8. 정렬 알고리즘(1) - 버블 정렬 개요 (0) | 2024.03.07 |
| [자료구조 with Python] 7. 선형 자료 구조 - 배열(6), Hash 충돌과 개방 주소법(Open Address) (0) | 2024.03.05 |




댓글