이번 포스팅은 정렬 알고리즘의 하나인 선택 정렬(Selection Sort)에 대한 내용이다. 지난 포스팅에서 살펴본 삽입 정렬과 매우 유사한 형태로 동작하는 코드이나, 처음 코드를 구현하는 단계라면 삽입 정렬보다 오히려 쉽다(삽입 정렬은 필자가 빠가라 이해를 잘못한 거고..).
바로 시작해보자.
1. 선택 정렬의 개요
선택 정렬은 삽입 정렬과 유사하다. 삽입 정렬처럼 원소 하나를 선택하고, 최소값을 판별하는 경우 자신의 왼쪽, 그렇지 않은 경우 자신의 오른쪽의 원소와 비교하는 것은 동일하다(오름차순을 기준으로). 다만 삽입 정렬과 큰 차이점이 있다면, 삽입 정렬은 선택하는 원소를 배열의 index 순서로 진행하나, 선택 정렬은 최소값을 선택한다는 차이점이 하나 있고, 선택한 값을 버블 정렬로 이동시키는 것이 아니라 가장 좌측의 원소와 대소 비교 후 자리 교대를 진행한다는 것이다.
(1) 세부 정렬 방식
귀찮긴 한데, 또 그림을 그려보자. 아래와 같은 배열이 있다(요즘엔 그림판 쓰기 너무 싫다).
7, 3, 5, 8, 4
우선 가장 좌측은 최소값을 배정할 것이기 때문에 가장 좌측 원소를 제외한 나머지 원소 중 최소값을 선택한다.
7, 3, 5, 8, 4
이제 선택된 최소값을 좌측의 Index에 위치한 원소와 대소 비교를 한다. 선택된 최소값인 3은 7보다 작으므로, 자리를 교대한다.
3, 7, 5, 8, 4
한 사이클이 완료되었다. 이제 가장 좌측에는 최소값이 배치되었기 때문에 1번 Index에 두 번 째로 작은 값을 배치해야한다. 따라서 1번 Index의 원소를 제외한 나머지 원소 중 최소값을 찾아 1번 Index와의 대소 비교 및 자리 교대를 진행한다.
3, 7, 5, 8, 4
-> 3, 4, 5, 8, 7
다음으로 세 번 째 작은 값을 2번 Index에 위치시켜야한다. 최소값을 선택해야하는 범위에서 가장 작은 값은 7이나 이미 3번 째 원소가 5이므로 자리 교대는 불필요하다.
3, 4, 5, 8, 7
따라서 그 다음 4번 Index 원소인 8과 대소 비교를 진행하며, 선택된 최소값 7은 4번 Index 원소인 8보다 작으므로 자리를 교대하게 된다.
3, 4, 5, 8, 7
3, 4, 5, 7, 8
주의해야 할 점은, 최소값 배치를 위해 대소 비교를 처음 진행했을 때, 선택된 최소값이 이미 자리를 선점한 값보다 큰 경우, 그 다음 우측에 있는 원소와의 비교 및 자리 교대를 진행해야한다는 것이다. 크게 이해가 어려운 부분은 아닌데, 간간히 이 로직을 잊어버리고 코드를 구현하게 되는 경우가 있어 주의가 필요하다.
(2) 안정 정렬 여부
선택 정렬은 삽입정렬과 유사하게 값을 선택하여 특정 방향의 Index에 위치하는 원소와 대소 비교를 진행하므로 유사하지만 삽입정렬이 안정 정렬(Stable Sorting)에 속하는 반면, 선택 정렬은 불안정 정렬(Unstable Sorting)에 속한다. 아래의 예시를 보자.
3, 4, 7, 6, 5, 5
-> 6, 5, 5 중 첫 최소값: 5
-> 3, 4, 5, 7, 6, 5
-> 3, 4, 5, 5, 7, 6
따라서 정렬 전 배열의 순서가 중요한 경우, 선택 정렬은 잘 사용하지 않는다.
(3) 선택 정렬의 시간 복잡도
선택 정렬의 정렬 세부 동작을 보면, 배열 내 최소값을 고르는 절차가 먼저 진행된다. 최소값의 선택은 배열을 스캔해야하기 때문에 for나 while과 같은 Loop 문이 1차적으로 동작한다.
그리고 최소값이 선택되면, 최소값이 위치한 Index로부터 좌측의 원소와 대소 비교를 진행해야하므로 다시 배열 일부분에 대한 스캔이 수행되어야한다. 즉, 최소값 선택을 위한 Loop 내에 대소 비교를 진행하는 Loop가 추가되어야하며, 이 때문에 선택 정렬의 시간 복잡도는 BigO 표기법으로 O(N^2)이 된다.
2. 선택 정렬의 구현
선택정렬은 필자가 삽입 정렬을 잘못 이해했듯이 이해를 잘못하지만 않는다면 구현하는데 크게 어려운 알고리즘은 아니다. 늘 그렇듯이 뼈대부터 만들어보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
def selection_sort(arr: list) -> None:
len_arr: int = len(arr)
left_limit: int = 0
for oidx in range(left_limit, len_arr):
min_idx = oidx
for iidx in range(oidx, len_arr):
if arr[min_idx] > arr[iidx]:
min_idx = iidx
print(f" * 최소값 검색 스캔 범위: {oidx}, {len_arr}")
print(f" * 범위 내 최소값: {arr[min_idx]}")
print()
left_limit += 1
|
cs |
지금은 최소값이 존재하더라도 가장 좌측의 값과 비교를 진행하지 않았기 때문에 최소값이 계속 3으로만 출력된다.

이제 선택된 최소값을 가장 좌측의 원소값과 비교하여 자리를 교체하는 코드를 작성하면 된다. 먼저 0번 Index 원소와의 비교 후, 스캔으로 선택한 최소값이 더 작다면 자리를 교체하고, 그렇지 않다면 다음 Index인 1번 원소와의 대소 비교를 진행한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
def selection_sort(arr: list) -> None:
len_arr: int = len(arr)
left_limit: int = 0
for oidx in range(left_limit, len_arr):
min_idx = oidx
for iidx in range(oidx, len_arr):
if arr[min_idx] > arr[iidx]:
min_idx = iidx
print(f" * 범위 내 최소값 Index: {min_idx}, 최소값: {arr[min_idx]}")
for cmp_idx in range(0, oidx):
if arr[cmp_idx] > arr[min_idx]:
arr[cmp_idx], arr[min_idx] = arr[min_idx], arr[cmp_idx]
break
print(arr)
left_limit += 1
|
cs |
최소값을 고르는 for 문 아래에 최소값 위치 이전의 원소들과 크기 비교 및 자리 교체를 위한 for 문이 하나 더 설정된 것이 보인다. 비교 및 교대와 관련된 코드를 Loop로 작성한 이유는 만약 가장 좌측의 값이 선택한 최소값과 교대되지 않는다면, 다음 Index의 원소와 비교를 진행해야하기 때문이다. for 문이 3개나 있어서 시간복잡도를 BigO(N^3)로 착각할 수 있지만, 두 개의 for문은 중첩이 아니라 별도로 동작하는 구조라 외부 Loop N번, 내부 2개의 Loop 2N번으로 2N^2이다.
결과는 아래와 같이 나온다.

3. 선택정렬은 불안정 정렬
아래의 실행 결과를 보자. 필자가 배열 내에 클래스 인스턴스를 넣어 self.num 값 순서대로 정렬하도록 만든 코드다.
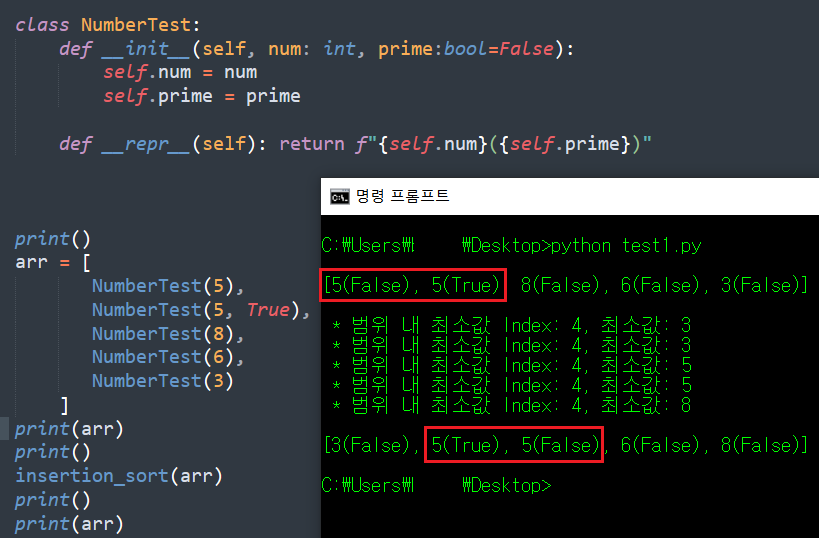
자세히 보면, 중복되는 값인 5가 배열의 가장 앞에 위치하고 있는 것이 보인다. 그런데, 이 두 값은 겉보기에는 동일한 값이지만 self.prime 값이 서로 다르게 지정되어 있다. 코드 수행 전의 self.prime 값이 False 인 5는 앞에, self.prime 값이 True인 5는 뒤에 위치해있다.
하지만 선택정렬을 수행하고 난 뒤의 결과를 보면, 이 두 값의 순서가 정렬 전과 다름을 확인할 수 있다. 즉, 일부 예외적인 상황에서 선택 정렬은, 동일한 값에 대해 정렬 이전의 순서와 정렬 이후의 순서가 변경될 여지가 있는 정렬 알고리즘이다.
따라서 데이터의 순서가 중요하나 순차정렬을 진행해야하는 경우에는 선택 정렬을 사용하지 않는다.
지금까지 필자가 다룬 세 개의 정렬(버블, 삽입, 선택)은 모두 Loop 문 두개를 중첩하여 돌리므로 시간 복잡도가 상당히 큰 편이다. 다음 포스팅에서는 소개한 세 정렬보다 조금 더 빠르게 정렬을 수행하도록 만드는 병합 정렬(Merge Sort)에 대해 알아보려한다.
'Python > Python Data Structure and Algorithm' 카테고리의 다른 글
| [자료구조 with Python] 13. 정렬 알고리즘(6), 퀵 정렬(Quick Sort) (0) | 2024.03.15 |
|---|---|
| [자료구조 with Python] 12 - 정렬 알고리즘(5), 병합 정렬(Merge Sort) (0) | 2024.03.13 |
| [자료구조 with Python] 10 - 정렬 알고리즘(3), 삽입 정렬(Insertion Sort) (0) | 2024.03.11 |
| [자료구조 with Python] 9. 정렬 알고리즘(2) - 버블 정렬과 Shaker 정렬 (0) | 2024.03.08 |
| [자료구조 with Python] 8. 정렬 알고리즘(1) - 버블 정렬 개요 (0) | 2024.03.07 |




댓글