선형 자료의 정렬과 관련된 내용을 지난 4개의 포스팅을 통해 살펴보았다. 조금만 정리를 하고 넘어가자면, 각각 버블, 삽입, 선택 정렬에 대한 내용이었으며 이들은 모두 중첩된 Loop 문을 사용하기에 시간 복잡도가 BigO(N^2)으로 나타난다. 그럼, 이런 의문이 들 수 밖에 없다.
"선형 자료를 정렬하는 더 빠른 방법은 없는 것일까요?"
왜 없을까. 머리 좋은 선구자들은 이미 자기들도 문제를 인지하고 머리 싸맸던 역사가 있다. 선형 정렬을 빠르게 할 수 있는 방법으로는 병합 정렬, 퀵 정렬, 쉘 정렬 등이 있는데, 그 중에 오늘은 병합 정렬(Merge Sort)라고 불리는 알고리즘에 대해 정리하려한다.
1. 병합 정렬(Merge Sort)의 개요
이름이 참 요상하다. 분명 정렬해야하는 배열은 하나인데, 뭘 합친다는 것일까? 뭔가를 만들어야하는데 도구가 없다면 가장 좋은 것은 있는 도구를 부셔서 재료를 만드는 것이다. 병합 정렬도 이렇게 생각하면 되는데, 정렬해야하는 병렬을 두 개로 쪼개어, 각자 정렬을 진행한 후 합친다는 개념이다.
말로는 복잡하니 또 다시 그려보자... 글 쓰기 귀찮으니 우선 짧은 배열부터 보자. 8, 4, 6, 9라는 숫자가 포함된 배열이 아래와 같이 존재한다.
8, 4, 6, 9
병합 정렬은 먼저 배열을 분해한다고 했으니, 이를 둘로 쪼개보자.
8, 4, 6, 9
↙ ↘
{8, 4} {6, 9}
여기서 배열을 또 나누어 보자.
8, 4, 6, 9
↙ ↘
{8, 4} {6, 9}
↙ ↘
{8}, {4} {6}, {9}
배열을 끝까지 나누었더니 원소가 1개인 배열이 4개 생긴다. 이제 나누어진 값들의 대소 비교를 진행하여 새 배열에 추가해보자. 작은 값이 먼저 들어가면 된다.
8, 4, 6, 9
↙ ↘
{8, 4} {6, 9}
↙ ↘
{8}, {4} {6}, {9}
↘ ↙
{4, 8} {6, 9}
첫 병합이 완료되면 2개의 원소를 가지는 2개 배열이 남게 된다. 이제 이 배열 내의 원소도 대소 비교를 통해 새 배열로 추가해보려한다.
첫 번째 비교 두 번째 비교 세 번째 비교 비교 종료
----------------------------------------------------------------------------------------------------------------------------------------------
{4, 8} -> 4 (0번 Index) 8 (1번 Index) 8 (1번 Index) N/A
{6, 9} -> 6 (0번 Index) 6 (0번 Index) 9 (1번 Index) 9 (1번 Index)
----------------------------------------------------------------------------------------------------------------------------------------------
신규 배열 -> { 4, 6, 8, 9 }
마지막 배열의 병합이 완료되면, 기존의 배열이 정렬된 값이 결과로 나타난다. 즉, 병합 정렬은 온전히 있는 배열을 최대한 분해하고, 분해한 배열을 정렬하여 합친다는, 직관적으로는 와 닿지 않는 알고리즘이다.
왜 이렇게 많이 나누어야할까? 그냥 배열 둘로 쪼개서 정렬하고 합치면 안될까? 물론 된다. 대신 시간 복잡도는 개선이 되지 않는다. 배열의 크기가 2개를 초과하는 배열을 온전한 상태에서 정렬하려면 앞서 살펴본 버블, 삽입, 정렬 방법 뿐인데, 이들은 이미 N^2이라는 크기의 시간 복잡도를 가지기 때문에 배열을 단순히 둘로 쪼개어 정렬하는 것으로는 시간 복잡도를 개선할 수 없는 것이 당연하다.
그럼, 병합 정렬은 어떨까? 병합 정렬은 두 배열의 크기를 비교하는 과정에서 단일 Loop문을 사용한다. 따라서 배열의 크기만큼의 시간 복잡도를 가지기 때문에(BigO(N)), 버블, 삽입, 선택 정렬과 비교하면 그만큼 속도가 빠르다.
진짜 그러한지, 구현 코드를 만들어 테스트 해보자.
2. 병합 정렬 구현 코드
뼈대부터 만들어보자. 병합정렬 역시 단순히 정렬된 결과만 만들어주면 되기에 함수로 작성한다. 그리고 함수 내에 정렬을 진행할 함수를 둘로 쪼개는 것까지 진행을 해보자.
|
1
2
3
4
5
6
7
8
9
10
|
def merge_sort(arr: list) -> None:
mid_idx = len(arr) // 2
left_arr = arr[:mid_idx]
right_arr = arr[mid_idx:]
print(f" * 앞 쪽 절반: {left_arr}")
print(f" * 뒤 쪽 절반: {right_arr}")
print(f" * 원래 배열: {arr}")
|
cs |
코드를 실행하면, 아래와 같이 배열의 절반이 쪼개져 출력되는 것을 확인할 수 있다.

우선 크기 비교는 둘째 치고, 한 번 더 배열을 쪼개어보려한다. 그런데, 이미 나누어진 배열을 또 쪼개려보니, 배열을 쪼개는데 사용했던 코드를 또 중복해서 사용해야된다는 문제가 생기고, 더 큰 문제는...

배열이 쪼개질수록 변수로 관리해야하는 포인트가 늘어난다는 것이다. 이런 문제를 피하기 위해, 이미 선언한 merge_sort() 함수를 함수 내부에서 다시 호출하는 재귀를 사용해야한다. 함수 내부에서 호출하는 merge_sort()는 나누어진 함수를 인자로 넣고, 함수의 크기가 1이면 아무 작업을 하지 않도록 설정해서 무한 루프가 도는 것을 피하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
# 재귀 확인용 변수
count = 0
def merge_sort(arr: list) -> None:
global count
# merge_sort 중단 확인
if len(arr) == 1:
return
print(f" * 배열 분회 횟수: {count}")
mid_idx = len(arr) // 2
left_arr = arr[:mid_idx]
right_arr = arr[mid_idx:]
print(f" * 앞 쪽 절반: {left_arr}")
print(f" * 뒤 쪽 절반: {right_arr}")
print(f" * 원래 배열: {arr}")
print()
count += 1
merge_sort(left_arr)
merge_sort(right_arr)
|
cs |
제대로 배열이 나뉘어졌는지 확인하기 위해 print() 문과 기타 변수를 넣어 코드가 복잡해보이는데, 실제로는 아래에 merge_sort()를 재귀로 호출하는 코드를 추가한 것과 재귀 함수를 중지하는 조건문을 추가한 것이 전부다. 위의 코드 결과는 아래와 같이, 원래의 배열이 최종 단계까지 뽀개어(?)지는 과정을 출력한다.
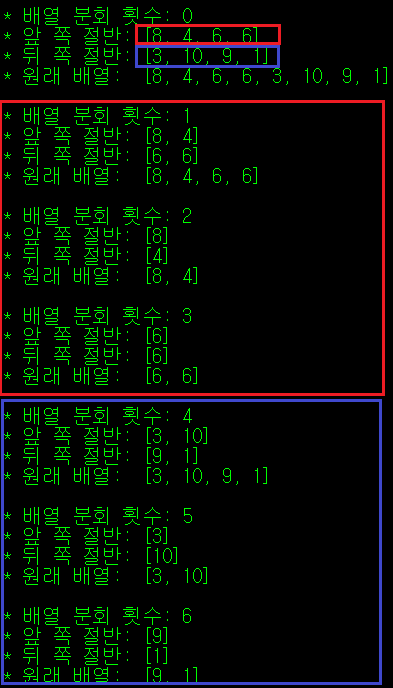
최종적으로 배열이 나누어지는 모습을 확인했으니, 가장 잘개 분해된 배열끼리의 비교를 통해 기존 배열을 정렬하는 방향으로 코드를 작성해보자.
(1) arr 변수를 변경해도 상관없는 경우: Python list의 call by reference 특성 이용
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
def merge_sort(arr: list) -> None:
global count
# merge_sort 중단 확인
if len(arr) == 1:
return
mid_idx = len(arr) // 2
left_arr = arr[:mid_idx]
right_arr = arr[mid_idx:]
merge_sort(left_arr)
merge_sort(right_arr)
# 크기 비교 및 정렬
tmp_arr = [ n for n in left_arr ]
len_tmp_arr = len(tmp_arr) # left_arr 복사본
len_right_arr = len(right_arr)
arr_cursor = 0
right_cursor = 0
tmp_cursor = 0 # left_arr 복사본의 배열에 사용할 cursor
while tmp_cursor < len_tmp_arr and right_cursor < len_right_arr:
if tmp_arr[tmp_cursor] <= right_arr[right_cursor]:
arr[arr_cursor] = tmp_arr[tmp_cursor]
tmp_cursor += 1
else:
arr[arr_cursor] = right_arr[right_cursor]
right_cursor += 1
arr_cursor += 1
# 조건이 있는 Loop문이므로 while로 작성해도 된다.
if tmp_cursor < len_tmp_arr:
for idx in range(tmp_cursor, len_tmp_arr):
arr[arr_cursor] = tmp_arr[idx]
arr_cursor += 1
# 사실 필요없는 코드: right_arr = arr[mid_idx:]
if right_cursor < len_right_arr:
for idx in range(right_cursor, len_right_arr):
arr[arr_cursor] = right_arr[idx]
arr_cursor += 1
# 분해된 배열의 정렬 결과 출력
print(arr)
|
cs |
갑자기 코드가 엄청 길어진 듯 한데, 병합 이전에 분류된 데이터에 대한 Loop를 진행함에 있어 필요한 변수가 많기 때문이다. 위에 필자가 작성한 코드는, 나누어진 배열을 비교한 뒤 값을 넣을 때, 나누어진 배열에 바로 넣는 방식을 선택했다.
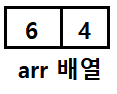
재귀 함수 초반부에 작성된 '배열 크기 1이상'의 조건에 걸리지 않는다면, 위와 같은 크기 2인 배열이 재귀함수의 호출부분 아래, 즉 위의 코드에서 주석으로 "크기 비교 및 정렬"이라고 작성된 코드를 수행하게 된다. 이 코드 내에 tmp_arr이라 불리는 새 배열을 선언하고, arr 배열의 전반 부분을 전부 Deep Copy로 복사했다. 만약, tmp_arr이라는 별도의 배열을 선언하지 않는다면, 혹은 선언을 하더라도 arr 전반 값을 단순히 참조만 하도록 (tmp_arr = arr[:mid_idx]) 코드를 작성하면 첫 원소 비교 이후 arr 값이 아래와 같이 변경된다.
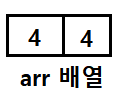
첫 대소 비교 후, arr[1]에 위치시켜야 할 값인 6이 자리교체로 인해 사라지기 때문에, 배열은 {4, 4}로 반환이 된다. 정렬은 {6, 4} 배열에 대해 진행하라고 던져놨더니, 값을 오히려 없애버리는 어이가 아리마셍한 상황이 벌어지는 것이다. 그렇기 때문에 실제 배열이 교체되는 자리에 위치한 원소들은, 배열 값 자체를 복사하여 다른 곳에 두고 참조할 수 있도록 만들어야한다.
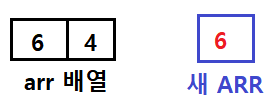
그리고 값의 비교는 새 배열에 복사한 arr의 좌측 배열 값과, 실제 arr의 우측 배열 값을 비교한 뒤, arr의 첫 부분부터 대체해 나가면 된다.
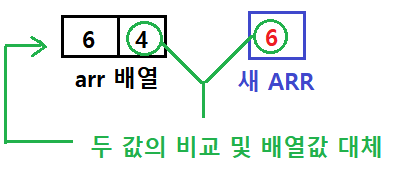
이렇게 정렬이 완료된 배열은 재귀 함수에서 별도로 return을 지정하지 않더라도 call by reference로 arr 값이 변경되는 효과로 나타난다. 위의 코드에서 비교 횟수만 추가로 출력하도록 print() 코드와 변수를 추가하면 아래와 같이 정렬이 16번만에 완료된 것을 확인할 수 있다.

(2) arr을 변경하고 싶지 않은 경우
만약 arr을 정렬 과정 외에 다른 함수에서도 매개인자로 사용해야한다고 가정해보자. 현재 위의 코드는 정렬이 완료되고나면 arr의 모양이 정렬 이전과 다른 형태를 띄게 된다. 방금 위에서 출력한 결과의 코드를 보자.
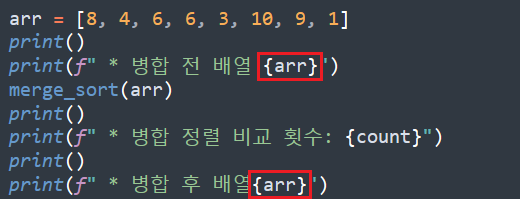
만약 merge_sort(arr) 아래에 변경 전의 arr 값을 사용해야하는 또 다른 함수가 존재한다면, 당연히 그 함수에서는 원하는 값이 돌아오지 못하게 된다. 따라서 기존의 배열 변화 없이 정렬된 결과만 받아야하는 경우, 새 배열을 만들어 정렬 값을 저장하고 새 배열을 돌려주는 방법을 사용해야한다.
바로 코드를 작성해보자. 우선, 나누어진 배열을 함수로 반환하는 코드부터 작성해보자.
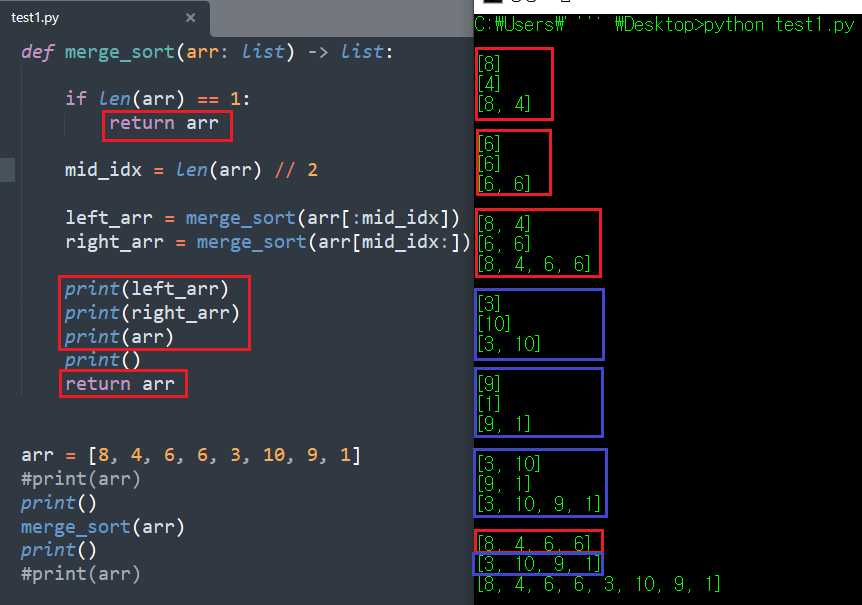
불필요한 부분을 싸그리 삭제하고 배열을 변환하는 방향으로 작성을 한 코드를 보면, 함수 내에 return arr이라는 반환이 추가되어 있음을 확인할 수 있다. 그리고 이 코드를 실행하면, 위와 같이 배열이 절반으로 쪼개어져 있다가 병합되어 다시 원상복구됨을 확인할 수 있다.
여기에 코드를 추가로 구현해보자. 값의 비교와 자리 교체를 통해 새 배열을 만들면 이 새 배열을 재귀 함수에서 반환할 수 있도록 만들어야 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
def merge_sort(arr: list) -> list:
if len(arr) == 1:
return arr
mid_idx = len(arr) // 2
left_arr = merge_sort(arr[:mid_idx])
right_arr = merge_sort(arr[mid_idx:])
# 비교 코드 작성
tmp_arr = [None] * len(arr)
left_cursor = 0
right_cursor = 0
tmp_cursor = 0
while left_cursor < len(left_arr) and right_cursor < len(right_arr):
if left_arr[left_cursor] <= right_arr[right_cursor]:
tmp_arr[tmp_cursor] = left_arr[left_cursor]
left_cursor += 1
else:
tmp_arr[tmp_cursor] = right_arr[right_cursor]
right_cursor += 1
tmp_cursor += 1
while left_cursor < len(left_arr):
tmp_arr[tmp_cursor] = left_arr[left_cursor]
tmp_cursor += 1
left_cursor += 1
while right_cursor < len(right_arr):
tmp_arr[tmp_cursor] = right_arr[right_cursor]
tmp_cursor += 1
right_cursor += 1
# 중간 결과 확인용 출력
print(tmp_arr)
return tmp_arr
|
cs |
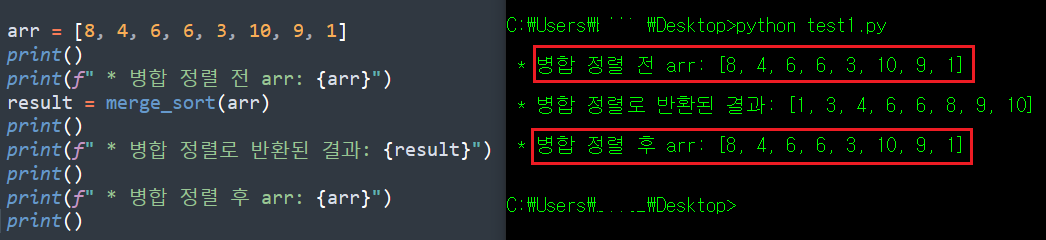
위 코드의 실행 결과는 아래와 같이 나타난다.
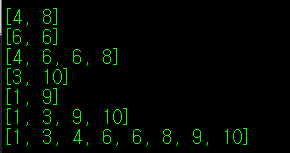
merge_sort()의 함수 인자로 사용한 arr에 직접적인 변화를 가하지 않고, 정렬할 값들을 tmp_arr에 넣어 반환하도록 만들었기 때문에, merge_sort()로 배열을 정렬하더라도 arr 값에는 변화가 없는 것을 확인할 수 있다.
구현의 마지막 단계... 코드가 지저분하니 바로 위의 코드만 조금만 정리해보자. 현재 필자가 구현한 코드는 배열을 반으로 갈라(?)버리는 기능과 대소 비교로 병합하는 과정이 하나의 함수 안에 존재하고 있다. 하나의 함수 안에 여러 기능을 구현하면 추후 수정이 필요한 경우 매우 귀찮아지니, 이 부분을 나누어보려한다.
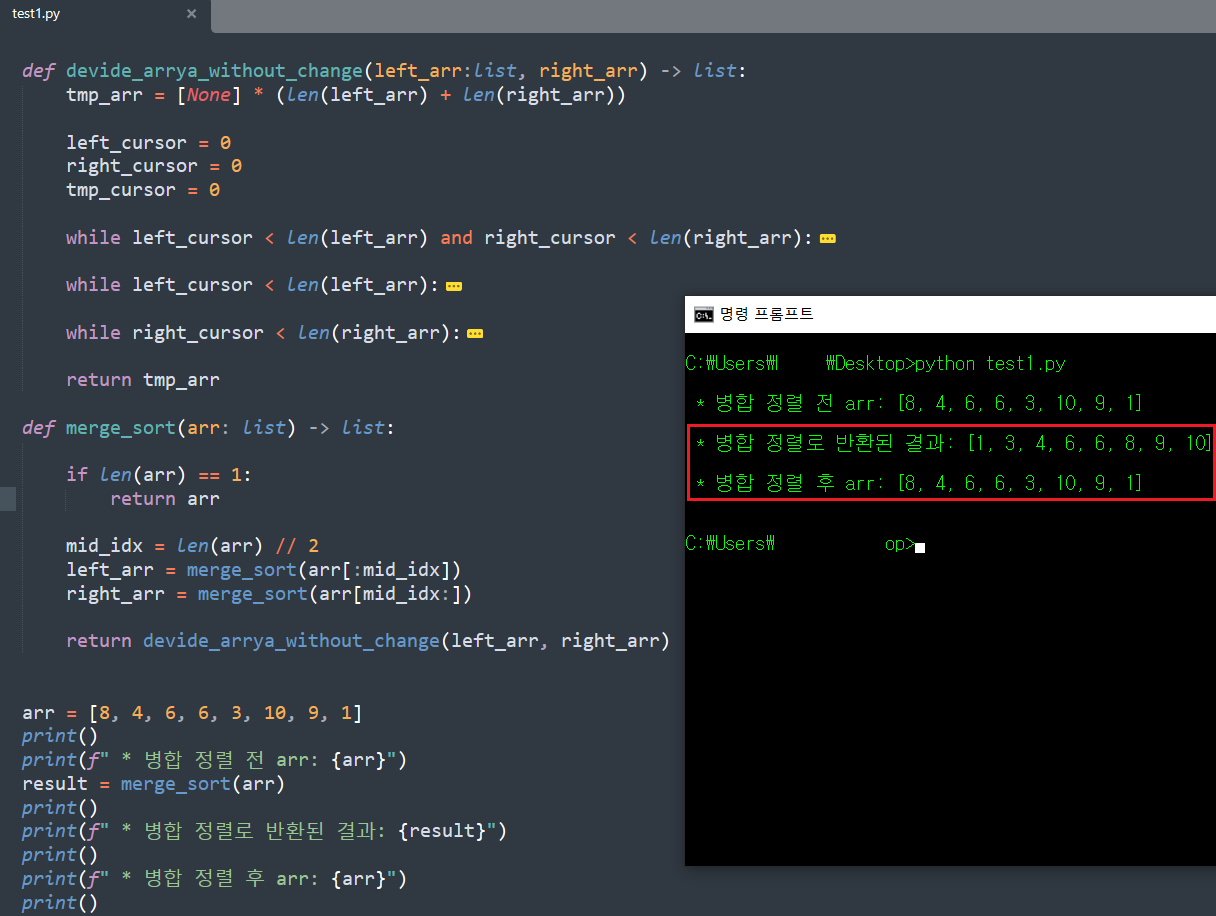
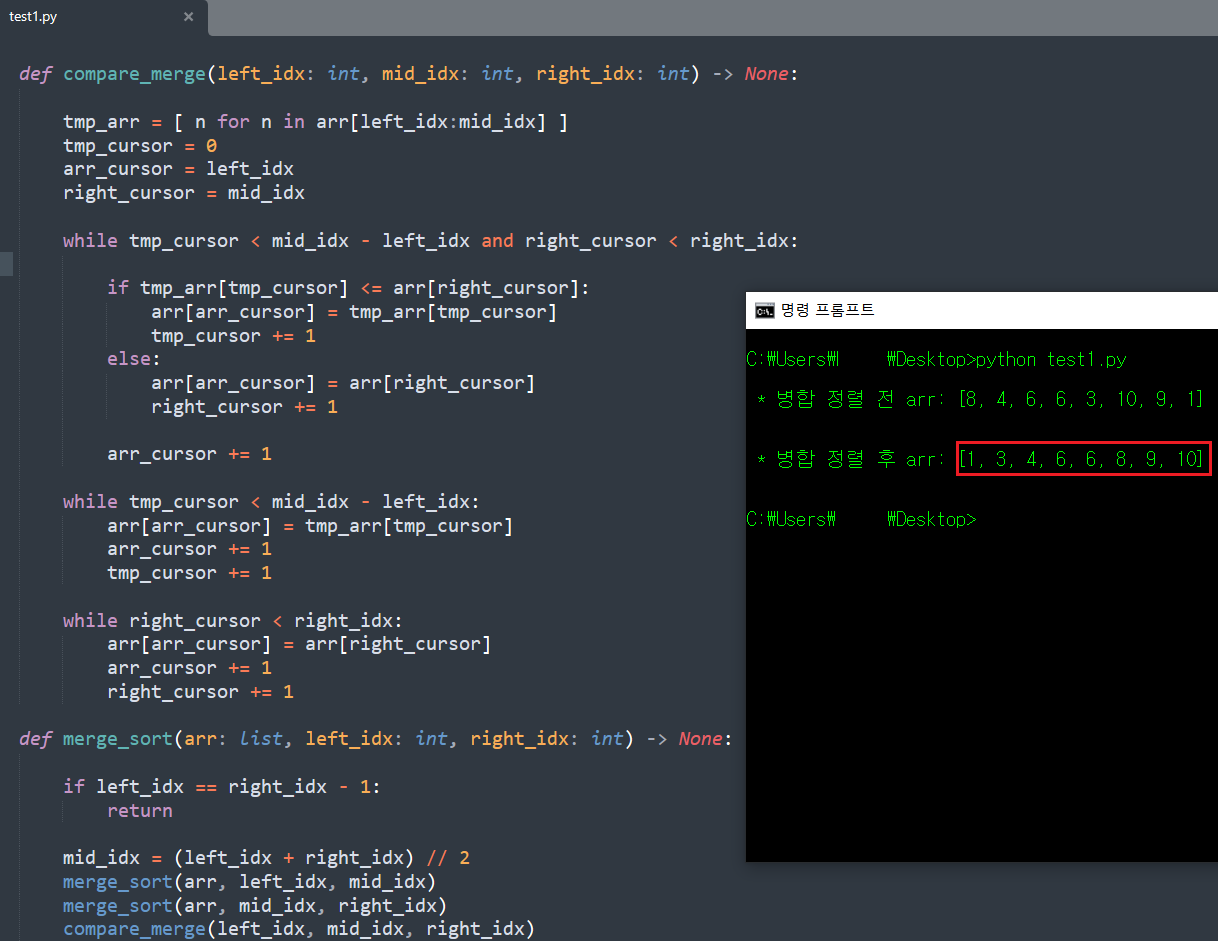
병합 정렬 함수 구현 시, 기존 배열을 수정하는 코드의 경우 함수 인자로 넘기는 값이 배열의 Index 위주인데 반해, 새 배열을 반환하는 코드는 함수 인자가 배열 위주라는 차이를 확인하자.
3. 진짜 마지막... 진짜 병합 정렬이 빠를까?
서두에 병합 정렬이 시간 복잡도 O(N)으로 수행되는 코드라고 언급했다. 버블, 삽입, 선택 정렬보다 수행 시간이 제곱근 정도의 값으로 단축된다는데, 시간을 측정해서 병합 정렬이 실제로 더 빠르게 정렬되는지 확인해보려한다.
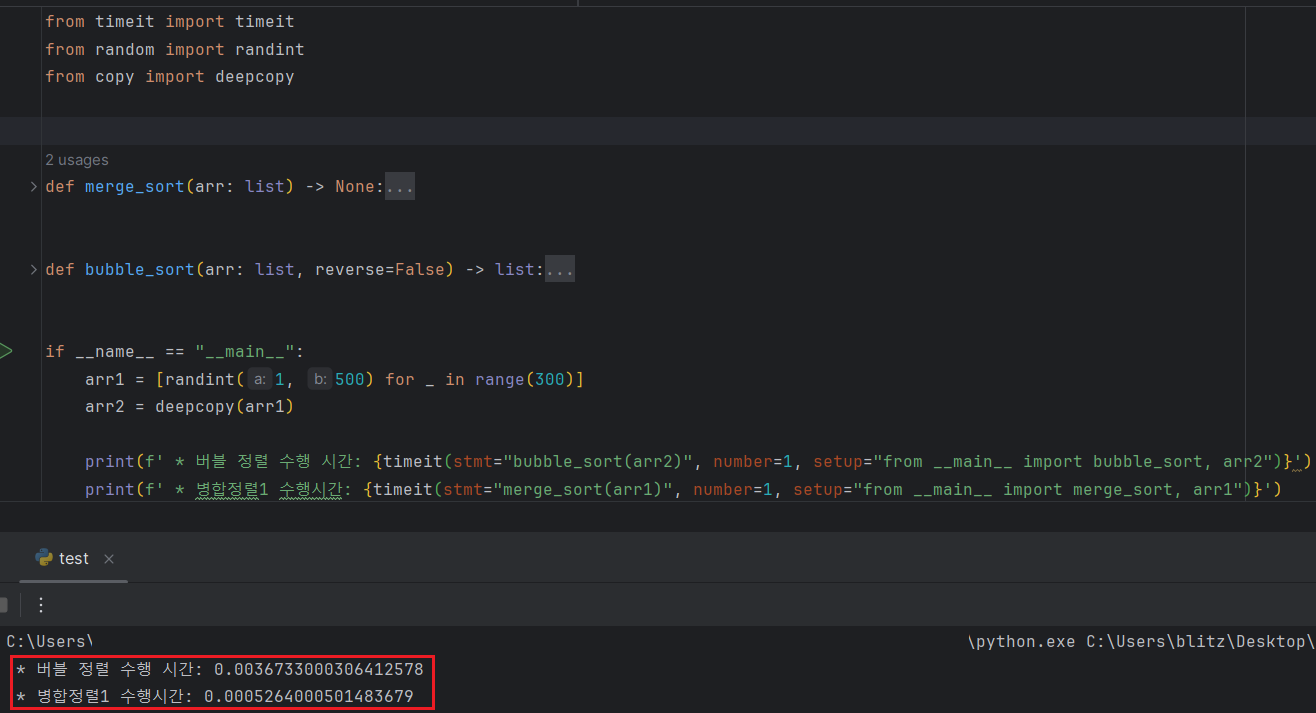
각 함수는 1부터 500 사이 무작위 숫자 300개의 배열을 정렬하는 것으로 진행했고, Timeit으로 각 함수의 1회 수행 시간을 측정한 것이다. 버블 정렬이 0.004초, 병합정렬이 0.001초로 무려 4배나 더 빠르게 계산하는 것을 확인할 수 있다.
다음 포스팅에서는 퀵 정렬(Quick Sort)에 대해 정리해보려한다.
END.
'Python > Python Data Structure and Algorithm' 카테고리의 다른 글
| [자료구조 with Python] 14. 정렬 알고리즘(7), 쉘 정렬(Shell Sort) (0) | 2024.03.18 |
|---|---|
| [자료구조 with Python] 13. 정렬 알고리즘(6), 퀵 정렬(Quick Sort) (0) | 2024.03.15 |
| [자료구조 with Python] 11 - 정렬 알고리즘(4), 선택 정렬(Selection Sort) (0) | 2024.03.12 |
| [자료구조 with Python] 10 - 정렬 알고리즘(3), 삽입 정렬(Insertion Sort) (0) | 2024.03.11 |
| [자료구조 with Python] 9. 정렬 알고리즘(2) - 버블 정렬과 Shaker 정렬 (0) | 2024.03.08 |




댓글